What Purpose Does Music Theory Serve?

When I first started taking music lessons in college, I thought that music theory was one of the most boring subjects in the world. My professors dutifully explained that music theory “is how musicians explain and describe the phenomena heard in a musical composition, while providing a system for musicians to communicate their ideas to one another.” I still wasn’t particularly happy with this explanation, until a good friend suggested that I start to think of music as a system of basic building blocks or elements. I suppose, it’s like the basic elements of language, and its combination of letters, words, vocabulary and grammar. Music theory, very basically, does the same thing for music, as it allows us to describe, compare and appreciate music at a much deeper level. In music practice, basic musical elements function like a composer’s toolbox, and music theory can help to explain how this musical vocabulary can be “formed into extended thoughts, which assume significance.” I thought it might be fun to write a little blog on rudimentary music theory in conventional music practice by looking at some basic elements of music, and provide examples from the vast repertoire of Western classical music.

Sound and Pitch

Music theory to improve your music practice

Sound is energy! It is the compression and rarefaction of molecules in a medium, most likely the atmosphere or water. And our ears function as a barometer that is highly sensitive to minute and very rapid changes in air pressure. When the compression and decompression of the atmosphere comes at regular, periodic intervals, it possesses what music theory calls “pitch,” which is either high or low. One such period of compression and decompression forms a cycle, and our ears can generally hear between roughly 20 and 15,000 cycles per seconds. You can sometimes see this expressed as “Hertz” or “Hz.” The greater the frequency of change, the higher the pitch. By convention, we say that when one pitch has twice the frequency of another, it lies an octave above. In other words, the pitch of 440 Hz sounds an octave above the pitch of 220 Hz, the pitch 660 Hz lies an octave above 330 Hz, and so forth. The distinctive flavor of most music results from the way in which we divide the octave into smaller segments. And one delicious way involves the division into six equal parts called whole tone. In music practice, Claude Debussy frequently uses whole tone scales as part of his mesmerizing and exotic soundscapes in his first volume of Préludes.

Claude Debussy: Préludes, “Voiles”

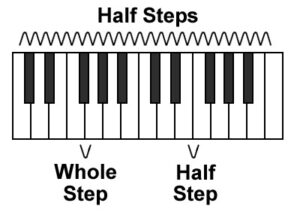
Music theory tells us that if we divided the octave into twelve equal parts, we arrive at intervals called semi tone or half steps. If in musical practice we then play a series of half steps directly in order they produce a chromatic or semi tone scale. When Johann Sebastian Bach sat down at the keyboard, his biographer tells, “He could do whatever he wanted. He had power over all keys and exploited the unique characters of sounds produced by the tuning of his time.” The so-called “Chromatic fantasia and fugue,” was already legendary in its day, and the nickname “Chromatic” basically refers to the three-part fugue. The theme moves in such mysterious chromatic steps that the overall harmony is only gradually established along the way.

Johann Sebastian Bach: Chromatic Fantasy and Fugue in D minor, BWV 903

Bartók recording folk songs

Folk music practice around the world seems to employ a very specific five-part partition of the octave. This five-part or pentatonic division does not consist of equal intervals. Instead, as music theory explains, we find a scale with three whole steps and two larger intervals equal to a whole step and half step combined. During the first part of the 20th century, the Hungarian composer Béla Bartók started to collect Hungarian folk music. He tirelessly traveled the countryside and recorded and transcribed the native musical expression of Slovakian, Rumanian, and Turkish language groups. In all, he published roughly 6000 folk songs in carefully annotated musical and scholarly editions, and he spent much time in trying to integrate these pentatonic melodies into becoming part of modern music. He even used them in his instructions for aspiring pianist.

Béla Bartók: “Pentatonic Melody”

Compositions can be based on steps that are smaller than a semi-tone, something that relies on a microtonal division of the octave. Many western cultures from at least the time of the ancient Greeks have preferred to divide the octave into an intermixture of five whole steps and two half steps; this seven-note partition of the octave bears the name diatonic. In a diatonic scale the two half steps occur asymmetrically according to the flavor or mode desired. When the half steps appear between third and fourth pitches and between the seventh and eighth pitches of the scale, we hear a major mode. I know, this sounds all pretty simplistic in terms of music theory, but just listen what Beethoven can do with a simple C-major scale.

Ludwig van Beethoven: Symphony No. 1 in C major, op. 21 “IV Finale: Adagio-Allegro”

whole and half steps - music theory for music practice

When the placement of half steps, according to music theory, is placed between the second and third pitches and between the fifth and sixth pitches of a scale, a minor mode is created. In music practice, music theory actually distinguishes between three scale patterns belonging to the minor mode. Whereas the major tonality is habitually associated with happiness and joy, the minor tonality is said to elicit sadness. These observations also seem rather simplistic, but it is clear that music has a direct connection to emotional states present in human beings. Pyotr Ilyich Tchaikovsky was rather depressed and frustrated when he worked on his 5th Symphony. He felt that he had lost his touch as a composer and that he needed to come up with an original and unique concept. His solution was to compose a main theme in the minor mode with a decided funeral character. This theme, sometimes called the “Fate Theme” sounds in all four movements and is gradually transforms into a triumphant march in the major mode at the end of the work.

Pyotr Ilyich Tchaikovsky: Symphony No. 5 in E minor, “Andante-Allegro con anima”

Personally, one of my favorite arrangements of pitches, which informed much of the popular music of the 20th century is called the “Blues scale.” It basically involves the drop in pitch on the third, fifth or seventh tone of the diatonic scale. This arrangement, with its characteristic “Blues notes,” arose in secular music with roots in African American folk forms. Before the word “Blues’ was actually attached to a musical style, it designated a state of sadness or melancholy. A scholar writes, “The content and definitions of blues have changed to fit shifts in musical fashions, technologies, performance styles, and audiences, but it has maintained its own identity and evolutionary history. With its deep roots and broad influence, blues is widely regarded as the foundation for nearly all later American popular forms.”

Billie Holiday: “Fine and Mellow”

Melody and Harmony

With some of the basic elements described by music theory behind us, let us focus our attention on a succession of individual pitches. When this happens in music, we are listening to a single line or melody. Melodies are described by their “shapes,” which can be level, undulating, falling, rising or arc-shaped. But wait, things are not that simple. Music theory is perfectly capable of describing the shape of a melody, but can it really define the almost unbelievable beauty of a Mozart melody? Mozart’s melodies, regardless if they are played by an instrument or expressed by a voice, almost always shine through their singing quality. His melodies are simple and basic, yet they are exquisite jewels. They are perfectly balanced, in complete equilibrium with the surrounding music, and above all, completely natural. There is a reason we consider Mozart the “most human of composers.”

Wolfgang Amadeus Mozart: Piano Concerto No. 21 in C Major, K. 467 “Andante”

In music practice, when we find pieces with more than one line playing at a time, we can also focus on the simultaneous sounding of pitches, or harmony. Groups of pitches sounded together form chords of two notes (dyads), three notes (triads), four notes (tetrads) and so forth. Music theory distinguishes the combinations further by the distance between pitches sounding simultaneously. The pitches may be only whole and half steps apart, or they may be spaced more distantly, every third note of the scale (tertian harmonies), every fourth note (quartal harmonies), every fifth note (quintal harmonies) and so forth. People in Western cultures from the sixteenth through the nineteenth centuries have generally preferred tertian harmonies as the most consonant. And for much of this period, at least from the end of the seventeenth century, tertian triads have formed the basis for the harmonic language of European and American art music, and they still form the basis for most popular music today.

Richard Wagner: Tristan and Isolde, “Vorspiel and Liebestod”

Texture and Temporal Elements

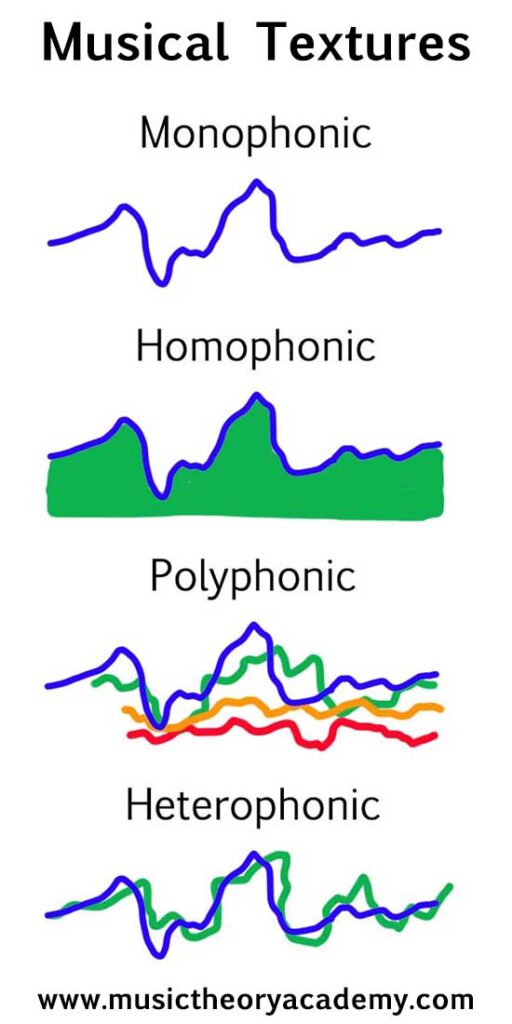
The texture of a given piece of music depends very much on the relationship between its various lines of melody. Some music consists solely of a single melodic line, or two or more melodic lines, which are identical to each other. This particular texture in music practice is called monophonic, or monophony. The predominant texture in Western classical, and most popular music around the world, unfolds in an arrangement that music theory calls homophonic texture or homophony. It involves a distinctive melodic line that is supported by accompanying lines of markedly lesser interest. We frequently find this kind of texture in songs for voice and piano or voice and orchestra.

Franz Schubert: “Heidenröslein”

In music practice, some pieces feature two or more equally distinctive melodies played at the same time. This particular texture is called polyphony, after a Greek word meaning “many sounds.” Polyphony is generally associated with counterpoint, an artful combination of distinct melodic lines. Polyphony has been described “as the outstanding characteristic that differentiates Western art music from the music of all cultures. While the special polyphony of ensembles in Asian music includes a type of melodic variation called heterophony, it is not truly contrapuntal in the Western sense. In his delightful “Music Box Waltz” Dmitri Shostakovich combines two charming independent melodies in a wonderful example of counterpoint and polyphony.

Dmitri Shostakovich: Ballet Suite No. 1, “Music Box Waltz”

Bach’s unfinished fugue in The Art of Fugue

When contrapuntal melodies imitate one another, music theory describes them as an example of imitative polyphony. The two most important musical forms of imitative polyphony are the canon, in which the interval of imitation stays the same throughout the piece, and the fugue, in which the interval of imitation is slightly modified. His contemporaries called Johann Sebastian Bach the “grand master of the fugue.” In fact, Bach was challenged by a colleague composer to “publish some triple fugues in invertible counterpoint,” meaning fugues with three subjects that could be combined in any and all possible ways. During the final decade of his life, Bach worked on a practical treatise called The Art of Fugue, a monumental project he left unfinished. “Bach had never been interested in theory textbooks preferring instead to place performance at the fore. He doesn’t enumerate rules, devises exercises or provides examples. Rather, he offers fully formed compositions that illustrate both the expressive and technical potential of fugal writing.”

Johann Sebastian Bach: The Art of Fugue, BWV 1080, “Contrapunctus 13”

Understande musical textures for your music practice

Extended pieces of music usually features interspersed polyphonic and homophonic sections, but in music practice, all musical sounds and silences separating them unfold in time. An important aspect of music involves manipulation of the listener’s perception of time. Most music marks the passage of time by means of a regular underlying pulse or beat. The beat is usually further organized into patterns of accentuation we call meter. The simplest grouping consists of one accented beat followed by one unaccented beat, which produces a duple meter when repeated incessantly as we find in many marches. A repeated grouping formed from one accented beat followed by two unaccented beats results in a triple meter, and both duple and triple belong to the class of simple meters. Compound meters result from superimposing metrical patterns on one another at the same time. For instance, a grouping of six pulses can be perceived as two groups of three beats, the first of which receives a primary accent while the second is unaccented. In other words, we perceive both duple and triple meters at the same time.

Johannes Brahms: Cello Sonata No 2, Op. 99 “Allegro appassionatao”

Score of Ligeti’s Etude

Music theory also identifies complex meters, which result from adding groups of two and three. For example, a group of five beats can be formed from one duple unit added to one triple unit or one triple unit added to a duple unit. And then we have something called “polymeter,” which results when two or more musical lines occur at the same time, each having a different meter. Finally, some pieces contain irregular meters, which shift patterns of accentuation every three or four measures. Meter tends to reinforce music’s ability to mark the regular passage of time, and on the musical graph, it is denoted by a time signature at the beginning of each piece or at each change of meter. To govern the speed of the basic pulse composers have traditionally adopted a series of Italian words with approximate meanings. Using the basic material provided by pitch and rhythm, and thus described by music theory, composers form melodies and harmonies into an infinite variety of more or less complex shapes that take on various kinds of further significance. In music practice, music theory can give structure and meaning to the magnificent edifice of musical expressions that are an intimate part of human nature.

For more of the best in classical music, sign up to our E-Newsletter

György Ligeti: Étude Nr. 1 “Désordre”